📚 Digital Logic Chapter 6: Registers and Counters 重點整理
📖 圖片檔案名稱對應表
請將PDF截圖存成以下檔名,放在HTML同一資料夾中:
fig6-1.png- 4-bit Register (Page 3)fig6-2.png- 4-bit Register with Parallel Load (Page 5)fig6-3.png- 4-bit Shift Register (Page 6)fig6-5.png- Serial Adder (Page 10)fig6-7.png- Universal Shift Register (Page 20)fig6-8.png- 4-bit Binary Ripple Counter (Page 24)fig6-10.png- BCD Ripple Counter (Page 27)fig6-12.png- 4-bit Synchronous Binary Counter (Page 31)fig6-14.png- Binary Counter with Parallel Load (Page 36)fig6-17.png- Ring Counter (Page 43)fig6-18.png- Johnson Counter (Page 46)
🔥 小考重點提醒
- 記住所有專有名詞的中英文對照
- 理解每個電路的工作原理和應用
- 熟悉狀態轉換和時序分析
- 掌握同步與非同步設計的差異
1. 基本定義 (Basic Definitions)
重要專有名詞 (中英對照)
- Register (暫存器/註冊器)
- Counter (計數器)
- Shift Register (移位暫存器)
- Parallel Load (平行載入)
- Serial Transfer (串列傳輸)
- Ripple Counter (漣波計數器)
- Synchronous Counter (同步計數器)
- Universal Shift Register (通用移位暫存器)
- Ring Counter (環狀計數器)
- Johnson Counter (約翰遜計數器)
📌 Register (暫存器)
一組flip-flop的組合,每個flip-flop能儲存一個bit的資訊。除了flip-flop外,還可能包含組合邏輯閘執行資料處理任務。
📌 Counter (計數器)
本質上是一個會按照預定狀態序列運作的register。
2. Registers (暫存器)
2.1 基本 4-bit Register
4-bit Register 電路圖
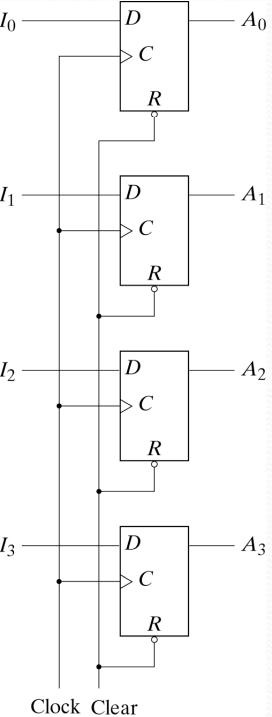
🔍 詳細工作原理解析
📍 Step 1: 電路組成分析
- 4個D-type flip-flop: 每個負責儲存1 bit資料
- 輸入端 I₀~I₃: 分別連接到各個flip-flop的D輸入
- 輸出端 A₀~A₃: 直接從各個flip-flop的Q輸出取得
- 共同Clock線: 連接到所有flip-flop的C輸入
- 共同Clear線: 連接到所有flip-flop的R(Reset)輸入
📍 Step 2: 操作流程詳解
- 資料準備階段: 將要儲存的4-bit資料放在I₀~I₃輸入端
- Clock觸發階段: 當Clock從低電位變高電位時(positive edge trigger)
- 資料載入階段: 所有flip-flop同時將D輸入的值載入到內部
- 資料輸出階段: 載入的資料立即出現在A₀~A₃輸出端
- 資料保持階段: 即使輸入改變,輸出依然保持直到下次Clock edge
📍 Step 3: 關鍵設計考量
- 為什麼用D flip-flop?
- D flip-flop具有透明的資料傳輸特性
- D輸入的值會在clock edge時直接傳到Q輸出
- 沒有複雜的控制邏輯需求
- 為什麼需要共同Clock?
- 確保所有bit同時載入(平行載入)
- 避免不同bit在不同時間載入造成的錯誤
- 提供系統同步基準
- Clear功能的作用?
- 系統初始化時將register清為0000
- Reset功能通常是asynchronous(不需要等Clock)
- 優先權高於正常的Clock操作
🔑 重要概念
- 平行載入 (Parallel Load): 所有bit同時載入,速度快
- 非破壞性讀取: 讀取輸出不會改變register內容
- 同步操作: 所有操作都與clock同步
- 資料保持: Clock邊緣之間資料保持穩定
2.2 Register with Parallel Load (平行載入暫存器)
4-bit Register with Parallel Load 電路圖
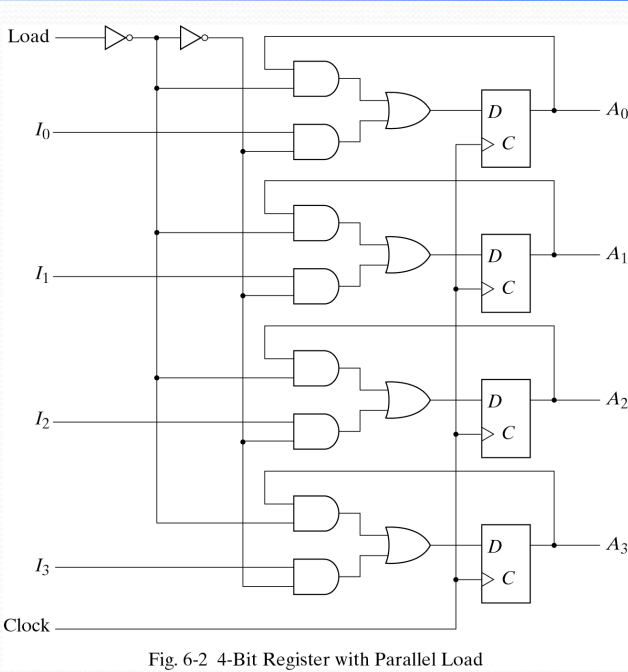
🔍 詳細工作原理解析
📍 Step 1: 電路組成分析
- 4個2-input OR gate: 每個flip-flop前面各有一個
- 8個2-input AND gate: 每個OR gate前面各有兩個
- 1個NOT gate: 將Load信號反相
- Load控制線: 控制是否載入新資料
- 回饋線 (Feedback): 將輸出回饋到輸入端
📍 Step 2: Load=1 時的操作流程
- Load信號=1 送入電路
- 上方AND gate啟用: Load=1使得輸入資料(I₀~I₃)可以通過
- 下方AND gate關閉: Load經NOT gate變成0,阻斷回饋路徑
- 新資料通過OR gate: 只有輸入資料能通過到達D flip-flop
- Clock edge觸發: 新資料載入到register中
- 結果: register內容更新為新的輸入資料
📍 Step 3: Load=0 時的操作流程
- Load信號=0 送入電路
- 上方AND gate關閉: Load=0使得輸入資料(I₀~I₃)被阻斷
- 下方AND gate啟用: Load經NOT gate變成1,啟用回饋路徑
- 原資料回饋: 輸出(A₀~A₃)經由回饋線回到OR gate
- Clock edge觸發: 原資料重新載入到register中
- 結果: register內容保持不變(No Change)
📍 Step 4: 為什麼不直接控制Clock?
⚠️ 控制Clock的問題:
- Propagation Delay不一致: 不同flip-flop的clock到達時間會不同
- Clock Skew問題: gate延遲造成clock信號偏移
- 破壞同步性: 無法保證所有flip-flop同時動作
- 設計複雜化: 需要考慮時序約束
✅ 控制D輸入的優點:
- 保持同步: 所有flip-flop依然共用同一個clean clock
- 時序簡單: 只需要滿足setup/hold time
- 設計可靠: 不會有clock skew問題
- 易於實現: 標準的組合邏輯設計
🔑 關鍵設計原則
- 永遠控制資料路徑,不控制時脈路徑
- 保持clock的完整性是同步設計的基礎
- 使用組合邏輯控制flip-flop的輸入
- No Change功能透過資料回饋實現
2.3 Shift Registers (移位暫存器)
4-bit Shift Register 電路圖
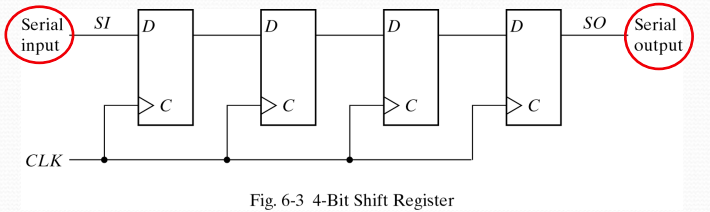
🔍 詳細工作原理解析
📍 Step 1: 電路拓撲分析
- 串聯結構: 4個D flip-flop串聯連接
- 資料流向: SI → FF1 → FF2 → FF3 → FF4 → SO
- Clock分配: 所有flip-flop共享同一個clock信號
- 傳播方向: 從左到右(向右移位)
📍 Step 2: 移位過程詳細分析
初始狀態假設: Register內容 = 1011
| Clock Pulse | SI輸入 | FF1(MSB) | FF2 | FF3 | FF4(LSB) | SO輸出 |
|---|---|---|---|---|---|---|
| Initial | - | 1 | 0 | 1 | 1 | 1 |
| Clock 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| Clock 2 | 1 | 1 | 0 | 1 | 0 | 0 |
| Clock 3 | 0 | 0 | 1 | 0 | 1 | 1 |
| Clock 4 | 1 | 1 | 0 | 1 | 0 | 0 |
📍 Step 3: 每個Clock Pulse的詳細動作
Clock 1 (SI=0) 的動作序列:
- Clock edge發生前: 各flip-flop準備接收新資料
- 資料準備:
- FF1的D輸入 = SI = 0
- FF2的D輸入 = FF1的Q輸出 = 1
- FF3的D輸入 = FF2的Q輸出 = 0
- FF4的D輸入 = FF3的Q輸出 = 1
- Clock edge觸發: 所有flip-flop同時載入D輸入的值
- 結果: 原來的1011變成0101,最右邊的1從SO輸出
📍 Step 4: 關鍵設計考量
- 為什麼要同步?
- 如果不同步,資料會在同一個clock內傳播多次
- 可能造成資料"追趕"現象
- 無法精確控制移位次數
- 移位的本質:
- 每個clock pulse,每個bit向右移動一個位置
- 最左邊位置被SI填入
- 最右邊位置的值從SO輸出並丟失
- 應用場景:
- 串列通訊(Serial Communication)
- 資料格式轉換(平行轉串列)
- 數學運算(乘除法的移位操作)
2.4 Serial Addition (串列加法)
Serial Adder 電路圖
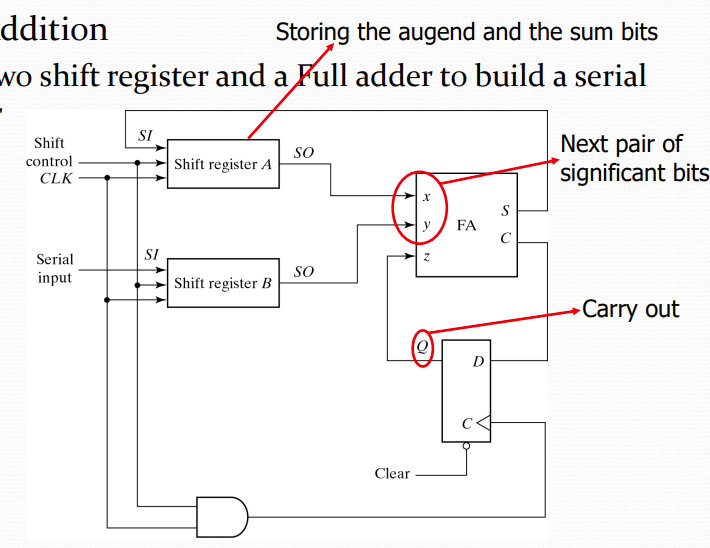
🔍 詳細工作原理解析
📍 Step 1: 電路組成分析
- Shift Register A: 儲存被加數(augend),後來儲存結果
- Shift Register B: 儲存加數(addend)
- Full Adder: 執行二進位加法運算
- Carry Flip-flop: 儲存進位值給下一位元使用
- Control Logic: 控制shift操作的時序
📍 Step 2: 初始化階段
- 資料載入:
- Register A = 被加數 (例如: 1011)
- Register B = 加數 (例如: 0110)
- 清除進位: Carry flip-flop清為0
- 準備開始: 從最低位元(LSB)開始加法
📍 Step 3: 逐位元加法過程
範例: 1011 + 0110 = ?
| Clock | Reg A (x) | Reg B (y) | Carry (z) | Sum (S) | New Carry | 說明 |
|---|---|---|---|---|---|---|
| Init | 1011 | 0110 | 0 | - | 0 | 初始狀態 |
| 1 | 1(LSB) | 0(LSB) | 0 | 1 | 0 | 1+0+0=1, carry=0 |
| 2 | 1 | 1 | 0 | 0 | 1 | 1+1+0=10, sum=0, carry=1 |
| 3 | 0 | 1 | 1 | 0 | 1 | 0+1+1=10, sum=0, carry=1 |
| 4 | 1(MSB) | 0(MSB) | 1 | 0 | 1 | 1+0+1=10, sum=0, carry=1 |
Full Adder 運算:
S = x ⊕ y ⊕ z
C = xy + xz + yz
S = x ⊕ y ⊕ z
C = xy + xz + yz
📍 Step 4: 每個Clock Cycle的詳細操作
在每個Clock Pulse期間:
- 輸出當前位元: Register A和B的SO分別提供x和y給Full Adder
- 加法運算: Full Adder計算 S = x ⊕ y ⊕ z (z是前一次的carry)
- 進位計算: Full Adder計算新的carry = xy + xz + yz
- 結果回饋: Sum bit (S) 回饋到Register A的SI輸入
- 進位儲存: 新的carry值儲存到Carry flip-flop
- 移位操作: 兩個register同時向右移位
📍 Step 5: 設計考量與特點
- 硬體節省:
- 只需要1個Full Adder(而非n個)
- 適合資源受限的應用
- 時間成本:
- 需要n個clock cycles處理n-bit數字
- 比parallel adder慢n倍
- 累積加法:
- 可以連續加多個數字
- 結果累積在Register A中
- 進位處理:
- Carry flip-flop是essential的
- 確保多位元加法的正確性
Serial Adder 控制方程式 (使用JK flip-flop for Carry):
J_Q = xy (當x=1且y=1時set carry)
K_Q = x'y' = (x + y)' (當x=0且y=0時reset carry)
S = x ⊕ y ⊕ Q (sum output)
J_Q = xy (當x=1且y=1時set carry)
K_Q = x'y' = (x + y)' (當x=0且y=0時reset carry)
S = x ⊕ y ⊕ Q (sum output)
2.5 Universal Shift Register (通用移位暫存器)
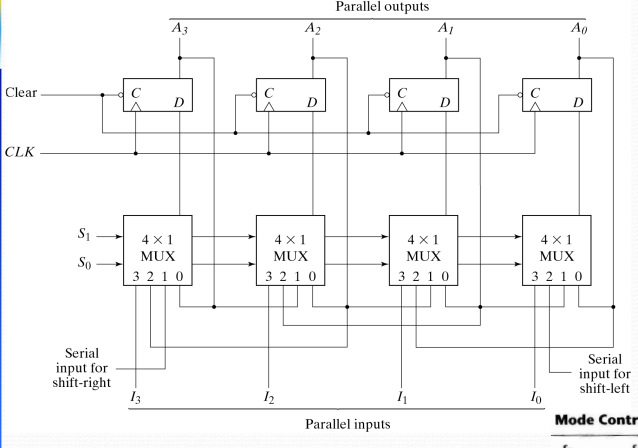
Universal Shift Register 電路圖
🔍 詳細工作原理解析
📍 Step 1: 電路架構分析
- 4×1 Multiplexer (每個stage一個): 選擇資料來源
- D Flip-flop (每個stage一個): 儲存資料
- Mode Control (S₁S₀): 控制操作模式
- 平行輸入/輸出: I₀~I₃ / A₀~A₃
- 串列輸入: 左移和右移的串列輸入
📍 Step 2: 4×1 MUX 輸入選擇分析
以A₁ stage為例,MUX的4個輸入:
- Input 0: A₁ (自己的輸出回饋) → No Change
- Input 1: A₀ (右邊neighbor的輸出) → Shift Right
- Input 2: A₂ (左邊neighbor的輸出) → Shift Left
- Input 3: I₁ (平行輸入) → Parallel Load
特殊情況處理:
- A₀ stage: Input 1 來自串列輸入(右移)
- A₃ stage: Input 2 來自串列輸入(左移)
📍 Step 3: 各種操作模式詳解
🔄 Mode 00: No Change
- MUX選擇: 所有MUX選擇Input 0
- 資料路徑: A₀→A₀, A₁→A₁, A₂→A₂, A₃→A₃
- 結果: 每個flip-flop輸出回饋到自己的輸入
- 效果: register內容保持不變
➡️ Mode 01: Shift Right
- MUX選擇: 所有MUX選擇Input 1
- 資料路徑: SI→A₃, A₃→A₂, A₂→A₁, A₁→A₀
- 結果: 所有資料向右移一位
- 效果: 左邊填入串列輸入,右邊資料移出
⬅️ Mode 10: Shift Left
- MUX選擇: 所有MUX選擇Input 2
- 資料路徑: A₀→A₁, A₁→A₂, A₂→A₃, SI→A₀
- 結果: 所有資料向左移一位
- 效果: 右邊填入串列輸入,左邊資料移出
📥 Mode 11: Parallel Load
- MUX選擇: 所有MUX選擇Input 3
- 資料路徑: I₀→A₀, I₁→A₁, I₂→A₂, I₃→A₃
- 結果: 平行輸入直接載入register
- 效果: 快速載入新的4-bit資料
📍 Step 4: 實際應用範例
情境: 將平行資料1101轉換為串列輸出
- Step 1: Mode=11, I₃I₂I₁I₀=1101 → Parallel Load
- Step 2: Mode=01, 右移4次,觀察A₀輸出
- 結果: A₀依序輸出 1→0→1→1 (LSB first)
情境: 串列資料轉平行資料
- Step 1: Mode=11, Load=0000 清空register
- Step 2: Mode=01, 串列輸入1011 (MSB first)
- Step 3: 4個clock後,A₃A₂A₁A₀=1011
🔑 Universal Shift Register 的七大功能
- Clear control - 清除register為0
- Clock input - 同步操作
- Shift-right control - 啟用右移和相關的serial I/O
- Shift-left control - 啟用左移和相關的serial I/O
- Parallel-load control - 啟用平行傳輸
- n parallel output lines - n條平行輸出線
- No-change control - 在clock存在時保持資訊不變
3. Counters (計數器)
3.1 Binary Ripple Counter (二進位漣波計數器)
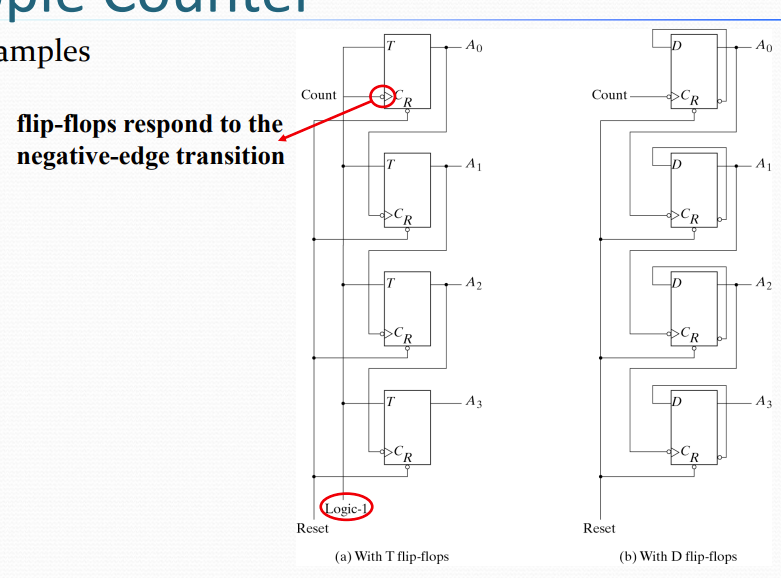
4-bit Binary Ripple Counter 電路圖
🔍 詳細工作原理解析
📍 Step 1: 電路拓撲分析
- 4個T flip-flop 串聯: 形成計數鏈
- 第一個FF: 由外部Count信號觸發
- 後續FF: 由前一個FF的輸出觸發
- 觸發方式: Negative edge triggered
- Reset線: 共同的異步復位
📍 Step 2: T Flip-flop 行為分析
- T=1時: 在clock edge時flip-flop會toggle(0→1 或 1→0)
- T=0時: flip-flop保持不變
- 本電路中: 所有T輸入都固定為1,所以每次clock edge都會toggle
📍 Step 3: 計數過程詳細分析
使用Negative Edge Trigger的原因:
- 當A₀從1→0時,才觸發A₁
- 當A₁從1→0時,才觸發A₂
- 以此類推...
| Count Pulse | A₃ | A₂ | A₁ | A₀ | 十進位值 | 變化說明 |
|---|---|---|---|---|---|---|
| Initial | 0 | 0 | 0 | 0 | 0 | Reset狀態 |
| 1 | 0 | 0 | 0 | 1 | 1 | 只有A₀ toggle |
| 2 | 0 | 0 | 1 | 0 | 2 | A₀: 1→0 觸發A₁ toggle |
| 3 | 0 | 0 | 1 | 1 | 3 | 只有A₀ toggle |
| 4 | 0 | 1 | 0 | 0 | 4 | A₀: 1→0, A₁: 1→0 觸發A₂ |
| ... | ... | ... | ... | ... | ... | ... |
| 15 | 1 | 1 | 1 | 1 | 15 | 最大計數值 |
| 16 | 0 | 0 | 0 | 0 | 0 | 溢出,回到0 |
📍 Step 4: 關鍵時序分析
為什麼叫"Ripple" Counter?
- 漣波效應: 計數變化像水波一樣從右向左傳播
- 非同步特性: 不是所有FF同時改變狀態
- 累積延遲: 每個FF都有propagation delay
Propagation Delay 問題:
- 單個FF延遲: 假設每個FF有10ns delay
- 4-bit counter總延遲: 最多40ns (4×10ns)
- Glitch問題: 在transition期間可能出現錯誤的中間狀態
- 頻率限制: 最高工作頻率受限於累積延遲
從0111到1000的詳細時序:
- t₀: Count pulse下降邊緣
- t₀+10ns: A₀從1變0 (0110)
- t₀+20ns: A₁從1變0 (0100)
- t₀+30ns: A₂從1變0 (0000)
- t₀+40ns: A₃從0變1 (1000) ← 最終穩定狀態
⚠️ Ripple Counter 的缺點
- 速度限制: 累積propagation delay限制最高頻率
- Glitch問題: transition期間出現錯誤狀態
- 不適合高速應用: 現代高速系統較少使用
- 解碼困難: glitch會影響狀態解碼電路
3.2 BCD Ripple Counter (BCD漣波計數器)
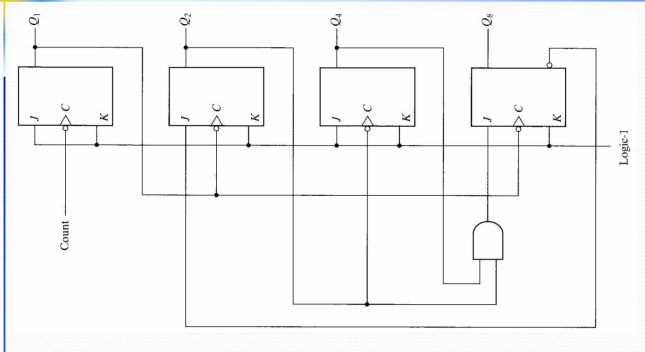
BCD Ripple Counter 電路圖
🔍 詳細工作原理解析
📍 Step 1: BCD Counter 特殊需求
- 計數範圍: 0000 到 1001 (0到9)
- 跳躍邏輯: 1001之後必須跳到0000,而非1010
- Reset邏輯: 需要特殊電路detect 1001狀態
- Decade counter: 每10個pulse重複一次
📍 Step 2: Reset邏輯設計
Detection Logic: 偵測1001狀態
- NAND gate輸入: Q₈ 和 Q₁
- 檢測條件: 當Q₈=1 且 Q₁=1時(即1001狀態)
- NAND輸出: 正常時為1,檢測到1001時變為0
- Reset action: 輸出0會reset所有flip-flop
為什麼只檢測Q₈和Q₁?
- 1001分析: Q₈=1, Q₄=0, Q₂=0, Q₁=1
- 唯一性: 在0-9範圍內,只有9(1001)有Q₈=Q₁=1
- 簡化電路: 不需要檢測Q₄和Q₂的0狀態
📍 Step 3: 計數序列詳細分析
| 十進位 | Q₈ | Q₄ | Q₂ | Q₁ | NAND輸出 | 說明 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 正常計數 |
| 1 | 0 | 0 | 0 | 1 | 1 | 正常計數 |
| 2 | 0 | 0 | 1 | 0 | 1 | 正常計數 |
| ... | ... | ... | ... | ... | ... | ... |
| 8 | 1 | 0 | 0 | 0 | 1 | 正常計數 |
| 9 | 1 | 0 | 0 | 1 | 0 | 觸發Reset! |
| 0 | 0 | 0 | 0 | 0 | 1 | Reset後回到0 |
📍 Step 4: Reset時序分析
從8到9到0的詳細過程:
- Count 9發生: 正常ripple過程到達1001
- NAND gate反應: 檢測到Q₈=Q₁=1,輸出變為0
- Asynchronous Reset: 所有flip-flop立即被reset
- 穩定到0000: counter回到初始狀態
- NAND恢復: 由於Q₈=Q₁=0,NAND輸出回到1
- 準備下次計數: counter準備好繼續計數
重要時序考量:
- Race condition: Reset必須夠快,避免count到1010
- Glitch duration: 1001狀態只存在很短時間
- 穩定性: Reset後系統必須穩定在0000
BCD Counter 狀態序列:
0000 → 0001 → 0010 → 0011 → 0100 → 0101 → 0110 → 0111 → 1000 → 1001 → 0000 (reset)
0000 → 0001 → 0010 → 0011 → 0100 → 0101 → 0110 → 0111 → 1000 → 1001 → 0000 (reset)
3.3 Synchronous Binary Counter (同步二進位計數器)
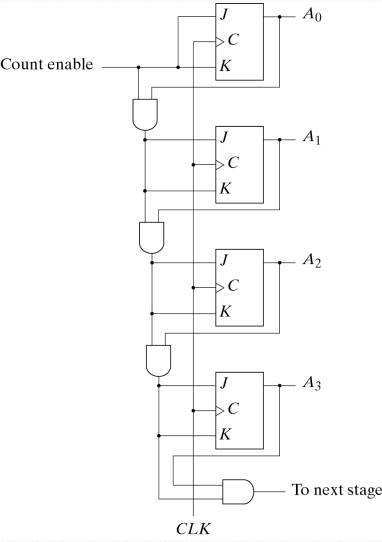
4-bit Synchronous Binary Counter 電路圖
🔍 詳細工作原理解析
📍 Step 1: 同步設計原理
- 共同Clock: 所有flip-flop連接到同一個clock
- 組合邏輯控制: 用AND gate決定何時toggle
- 無Ripple效應: 所有變化同時發生
- JK Flip-flop: 利用J=K=1時的toggle特性
📍 Step 2: Toggle條件設計
二進位計數的規律:
- A₀ (LSB): 每個clock pulse都要toggle
- A₁: 當A₀=1時才toggle
- A₂: 當A₁=A₀=1時才toggle
- A₃ (MSB): 當A₂=A₁=A₀=1時才toggle
JK Flip-flop控制邏輯:
- J₀ = K₀ = Count Enable
- J₁ = K₁ = A₀ · Count Enable
- J₂ = K₂ = A₁ · A₀ · Count Enable
- J₃ = K₃ = A₂ · A₁ · A₀ · Count Enable
📍 Step 3: 電路實現細節
AND Gate層次結構:
- 第一層: Count Enable直接到A₀
- 第二層: A₀ AND Count Enable到A₁
- 第三層: (A₁ AND A₀) AND Count Enable到A₂
- 第四層: (A₂ AND A₁ AND A₀) AND Count Enable到A₃
為什麼這樣設計?
- 效率考量: 避免重複計算相同的AND結果
- 延遲最小化: 每一層只增加一個gate delay
- 擴展性: 容易擴展到更多bit
📍 Step 4: 計數過程分析
範例: 從0111到1000的轉換
| Flip-flop | 目前狀態 | J輸入 | K輸入 | 下個狀態 | 說明 |
|---|---|---|---|---|---|
| A₀ | 1 | 1 | 1 | 0 | Count Enable=1,所以toggle |
| A₁ | 1 | 1 | 1 | 0 | A₀=1且Count Enable=1,所以toggle |
| A₂ | 1 | 1 | 1 | 0 | A₁=A₀=1且Count Enable=1,所以toggle |
| A₃ | 0 | 1 | 1 | 1 | A₂=A₁=A₀=1且Count Enable=1,所以toggle |
結果: 0111 → 1000 (7 → 8)
📍 Step 5: 同步vs非同步比較
✅ Synchronous Counter優點
- 速度快: 無累積propagation delay
- 無Glitch: 所有變化同時發生
- 易於控制: 可以精確控制計數時機
- 適合高速: 頻率限制主要來自flip-flop本身
❌ Synchronous Counter缺點
- 電路複雜: 需要額外的AND gate
- 功耗較高: 更多gate在工作
- 設計困難: 需要仔細的邏輯設計
- 成本較高: 更多硬體組件
3.4 Binary Counter with Parallel Load (具平行載入的二進位計數器)
Binary Counter with Parallel Load 電路圖
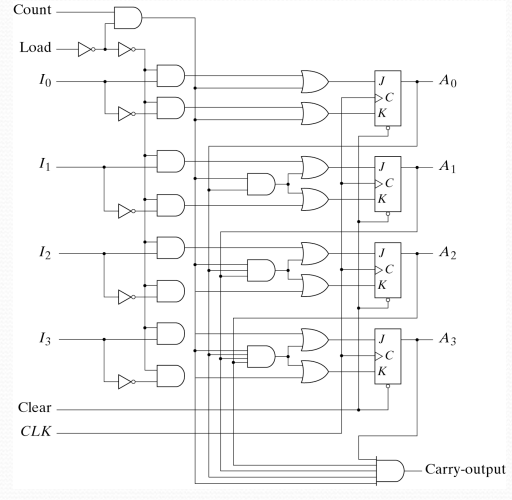
🔍 詳細工作原理解析
📍 Step 1: 多功能控制需求
- 平行載入: 快速設定初始值
- 計數功能: 正常二進位計數
- 保持功能: 維持目前狀態
- 清除功能: 歸零重置
📍 Step 2: 控制信號優先權
| Clear | CLK | Load | Count | Function |
|---|---|---|---|---|
| 0 | X | X | X | Clear to 0 (最高優先權) |
| 1 | ↑ | 1 | X | Load inputs (第二優先權) |
| 1 | ↑ | 0 | 1 | Count next binary state |
| 1 | ↑ | 0 | 0 | No change |
📍 Step 3: 複雜控制邏輯設計
每個flip-flop的輸入邏輯:
- 當Load=1時: J=I, K=I' (載入平行輸入)
- 當Load=0且Count=1時: 正常計數邏輯
- 當Load=0且Count=0時: J=0, K=0 (no change)
以A₀為例的完整邏輯:
J₀ = Load·I₀ + Load'·Count
K₀ = Load·I₀' + Load'·Count
K₀ = Load·I₀' + Load'·Count
以A₁為例的完整邏輯:
J₁ = Load·I₁ + Load'·Count·A₀
K₁ = Load·I₁' + Load'·Count·A₀
K₁ = Load·I₁' + Load'·Count·A₀
📍 Step 4: 實際應用場景
場景1: 預設計數器
- Load=1: 載入起始值(例如: 1100)
- Load=0, Count=1: 從1100開始計數
- 結果: 1100→1101→1110→1111→0000→...
場景2: 可程式化分頻器
- 設定分頻比: Load=1,載入(16-N)
- 計數到溢出: Count=1,計數N次後溢出
- 自動重載: 溢出時自動重新載入
- 結果: 產生1/N分頻輸出
場景3: 倒數計時器
- 載入時間值: Load=1,載入倒數起始值
- 倒數計數: 使用down counter邏輯
- 零檢測: 檢測到0000時產生timeout信號
3.5 Ring Counter (環狀計數器)
Ring Counter 電路圖

🔍 詳細工作原理解析
📍 Step 1: 基本原理
- 環狀連接: 最後一個FF的輸出連回第一個FF的輸入
- 單一"1"循環: 只有一個FF為1,其他都為0
- 移位操作: 每個clock pulse,"1"向右移動一位
- 週期性: n個FF產生n個不同的timing signals
📍 Step 2: 初始化的重要性
正確初始化: 1000
- 方法1: 第一個FF preset to 1,其他clear to 0
- 方法2: 全部clear後,第一個FF set to 1
- 結果: 產生有效的cycling pattern
錯誤初始化的後果:
- 全0 (0000): 永遠保持0000,沒有活動
- 多個1: 產生非預期的pattern
- 全1 (1111): 永遠保持1111,沒有區別
📍 Step 3: 狀態序列分析
| Clock | T₃ | T₂ | T₁ | T₀ | Active Output |
|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | T₃ |
| 1 | 0 | 1 | 0 | 0 | T₂ |
| 2 | 0 | 0 | 1 | 0 | T₁ |
| 3 | 0 | 0 | 0 | 1 | T₀ |
| 4 | 1 | 0 | 0 | 0 | T₃ (回到初始) |
📍 Step 4: 應用: Timing Signal Generation
微處理器控制應用:
- T₀: Fetch instruction
- T₁: Decode instruction
- T₂: Execute instruction
- T₃: Write back result
通訊協定控制:
- T₀: Send start bit
- T₁: Send data bit 0
- T₂: Send data bit 1
- T₃: Send stop bit
3.6 Johnson Counter (約翰遜計數器)
Johnson Counter 電路圖

🔍 詳細工作原理解析
📍 Step 1: Switch-tail Ring Counter原理
- 關鍵差異: 最後一個FF的complement輸出回饋到第一個FF
- 狀態數量: n個FF可產生2n個不同狀態
- 回饋邏輯: NOT gate提供complemented feedback
- 填充模式: 先填入1,再填入0
📍 Step 2: 詳細狀態轉換分析
| Clock | A | B | C | E | 說明 | 解碼邏輯 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 全為0 | A'E' |
| 1 | 1 | 0 | 0 | 0 | E'(1)進入A | AB' |
| 2 | 1 | 1 | 0 | 0 | A(1)進入B | BC' |
| 3 | 1 | 1 | 1 | 0 | B(1)進入C | CE' |
| 4 | 1 | 1 | 1 | 1 | C(1)進入E,全為1 | AE |
| 5 | 0 | 1 | 1 | 1 | E'(0)進入A | A'B |
| 6 | 0 | 0 | 1 | 1 | A(0)進入B | B'C |
| 7 | 0 | 0 | 0 | 1 | B(0)進入C | C'E |
📍 Step 3: 解碼邏輯設計規律
解碼規律分析:
- 全0狀態 (0000): 兩端的complement → A'E'
- 全1狀態 (1111): 兩端的normal → AE
- 其他狀態: 相鄰的1,0或0,1 pattern
相鄰位元檢測:
- AB': 檢測A=1, B=0的pattern
- BC': 檢測B=1, C=0的pattern
- CE': 檢測C=1, E=0的pattern
- A'B: 檢測A=0, B=1的pattern
- B'C: 檢測B=0, C=1的pattern
- C'E: 檢測C=0, E=1的pattern
📍 Step 4: 自我修正電路設計
問題: Invalid State處理
- 16個可能狀態: 4-bit系統有16個狀態
- 8個有效狀態: Johnson counter只用8個
- 8個無效狀態: 需要處理這些狀態
解決方案: 修改D_C輸入
D_C = (A + C)B
修正邏輯說明:
- 正常操作時: (A + C)B = B (因為A或C必有一個為1)
- 無效狀態時: 強制導向有效狀態
- 自我修正: 經過幾個clock後回到正常序列
🔑 Johnson Counter vs Ring Counter 比較
| 特性 | Ring Counter | Johnson Counter |
|---|---|---|
| Flip-flop數量 | n | n |
| 狀態數量 | n | 2n |
| 效率 | 1 state / FF | 2 states / FF |
| 解碼複雜度 | 不需解碼 | 需要2-input gate |
| 初始化 | 必須精確 | 相對容錯 |
4. 重要設計比較總結
4.1 Speed vs Hardware Trade-off
⚡ 高速設計
- Synchronous Counter - 無propagation delay累積
- Parallel Operations - 所有bit同時處理
- Combinational Logic - 直接邏輯運算
💰 節省硬體
- Ripple Counter - 最簡單的連接
- Serial Operations - 重複使用相同電路
- Johnson Counter - 最大化flip-flop效率
4.2 各種Counter的應用場景
🎯 選擇指南
- Ripple Counter: 低速、低成本應用(如數位時鐘的秒計數)
- Synchronous Counter: 高速、精密控制(如CPU時序產生)
- BCD Counter: 十進位顯示應用(如數位計時器顯示)
- Ring Counter: 狀態機控制(如洗衣機控制序列)
- Johnson Counter: 高效timing產生(如多相時脈產生)
5. 重要設計原則
🔍 Digital Design Best Practices
📍 原則1: Clock Domain Management
- 保持clock完整性: 不要在clock路徑上加logic gate
- 同步設計優先: 盡量使用synchronous邏輯
- Clock skew最小化: 確保所有FF同時收到clock
- Reset策略: 提供可靠的系統初始化機制
📍 原則2: State Management
- 定義所有狀態: 包括valid和invalid states
- State recovery: 設計從invalid state回到valid state的路徑
- 初始化考量: 確保系統有明確的起始狀態
- 狀態編碼: 選擇適當的state encoding方式
📍 原則3: Timing Considerations
- Setup/Hold time: 滿足flip-flop的timing requirements
- Propagation delay: 考慮組合邏輯的延遲
- Critical path: 識別並優化最長的邏輯路徑
- Metastability: 避免非同步輸入造成的亞穩態
🔥 小考終極應試攻略
📝 必考重點預測:
- 電路分析題: 給電路圖,分析工作原理
- 狀態轉換表: 寫出counter的state sequence
- 時序圖分析: 根據timing diagram回答問題
- 設計選擇題: 比較不同設計方法的優缺點
- 邏輯設計: 設計滿足特定需求的簡單電路
⚡ 快速解題策略:
- 看到register → 立即想到: 平行載入、資料儲存、D flip-flop
- 看到shift register → 立即想到: 串列傳輸、移位方向、資料流
- 看到ripple counter → 立即想到: 非同步、cascade、propagation delay
- 看到synchronous counter → 立即想到: 共同clock、AND gate、同時變化
- 看到timing diagram → 注意: clock edge、setup time、資料變化
💡 終極記憶法則:
"快同慢異,存移算計"
快速用同步,慢速用非同步
存儲用Register,移位用Shift Register
運算用Serial Adder,計數用Counter
快速用同步,慢速用非同步
存儲用Register,移位用Shift Register
運算用Serial Adder,計數用Counter
🎯 考前檢查清單:
- ✅ 所有專有名詞中英對照已熟記
- ✅ 每種電路的基本工作原理已理解
- ✅ 同步vs非同步的區別已掌握
- ✅ 常見的狀態轉換序列已熟悉
- ✅ 設計原則和應用場景已了解
⚠️ 常見陷阱提醒
- 不要混淆: Serial vs Parallel, Synchronous vs Asynchronous
- 注意細節: Clock edge方向, Reset信號極性
- 狀態分析: 確實了解每個clock cycle的變化
- 設計選擇: 根據需求選擇合適的電路類型
🎓 準備充分,小考必勝!
記住:理解原理比死記硬背更重要!
Good Luck! 💪